| Figure 3.1: Page Table Layout |



Linux layers the machine independent/dependent layer in an unusual manner in comparison to other operating systems [CP99]. Other operating systems have objects which manage the underlying physical pages such as the pmap object in BSD. Linux instead maintains the concept of a three-level page table in the architecture independent code even if the underlying architecture does not support it. While this is conceptually easy to understand, it also means that the distinction between different types of pages is very blurry and page types are identified by their flags or what lists they exist on rather than the objects they belong to.
Architectures that manage their Memory Management Unit (MMU) differently are expected to emulate the three-level page tables. For example, on the x86 without PAE enabled, only two page table levels are available. The Page Middle Directory (PMD) is defined to be of size 1 and “folds back” directly onto the Page Global Directory (PGD) which is optimised out at compile time. Unfortunately, for architectures that do not manage their cache or Translation Lookaside Buffer (TLB) automatically, hooks for machine dependent have to be explicitly left in the code for when the TLB and CPU caches need to be altered and flushed even if they are null operations on some architectures like the x86. These hooks are discussed further in Section 3.8.
This chapter will begin by describing how the page table is arranged and what types are used to describe the three separate levels of the page table followed by how a virtual address is broken up into its component parts for navigating the table. Once covered, it will be discussed how the lowest level entry, the Page Table Entry (PTE) and what bits are used by the hardware. After that, the macros used for navigating a page table, setting and checking attributes will be discussed before talking about how the page table is populated and how pages are allocated and freed for the use with page tables. The initialisation stage is then discussed which shows how the page tables are initialised during boot strapping. Finally, we will cover how the TLB and CPU caches are utilised.
Each process a pointer (mm_struct→pgd) to its own Page Global Directory (PGD) which is a physical page frame. This frame contains an array of type pgd_t which is an architecture specific type defined in <asm/page.h>. The page tables are loaded differently depending on the architecture. On the x86, the process page table is loaded by copying mm_struct→pgd into the cr3 register which has the side effect of flushing the TLB. In fact this is how the function __flush_tlb() is implemented in the architecture dependent code.
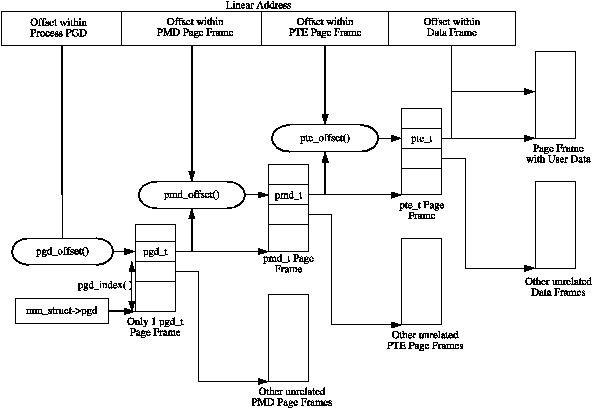
Each active entry in the PGD table points to a page frame containing an array of Page Middle Directory (PMD) entries of type pmd_t which in turn points to page frames containing Page Table Entries (PTE) of type pte_t, which finally points to page frames containing the actual user data. In the event the page has been swapped out to backing storage, the swap entry is stored in the PTE and used by do_swap_page() during page fault to find the swap entry containing the page data. The page table layout is illustrated in Figure 3.1.
Figure 3.1: Page Table Layout
Any given linear address may be broken up into parts to yield offsets within these three page table levels and an offset within the actual page. To help break up the linear address into its component parts, a number of macros are provided in triplets for each page table level, namely a SHIFT, a SIZE and a MASK macro. The SHIFT macros specifies the length in bits that are mapped by each level of the page tables as illustrated in Figure 3.2.
Figure 3.2: Linear Address Bit Size Macros
The MASK values can be ANDd with a linear address to mask out all the upper bits and is frequently used to determine if a linear address is aligned to a given level within the page table. The SIZE macros reveal how many bytes are addressed by each entry at each level. The relationship between the SIZE and MASK macros is illustrated in Figure 3.3.
Figure 3.3: Linear Address Size and Mask Macros
For the calculation of each of the triplets, only SHIFT is important as the other two are calculated based on it. For example, the three macros for page level on the x86 are:
5 #define PAGE_SHIFT 12 6 #define PAGE_SIZE (1UL << PAGE_SHIFT) 7 #define PAGE_MASK (~(PAGE_SIZE-1))
PAGE_SHIFT is the length in bits of the offset part of the linear address space which is 12 bits on the x86. The size of a page is easily calculated as 2PAGE_SHIFT which is the equivalent of the code above. Finally the mask is calculated as the negation of the bits which make up the PAGE_SIZE - 1. If a page needs to be aligned on a page boundary, PAGE_ALIGN() is used. This macro adds PAGE_SIZE - 1 to the address before simply ANDing it with the PAGE_MASK to zero out the page offset bits.
PMD_SHIFT is the number of bits in the linear address which are mapped by the second level part of the table. The PMD_SIZE and PMD_MASK are calculated in a similar way to the page level macros.
PGDIR_SHIFT is the number of bits which are mapped by the top, or first level, of the page table. The PGDIR_SIZE and PGDIR_MASK are calculated in the same manner as above.
The last three macros of importance are the PTRS_PER_x which determine the number of entries in each level of the page table. PTRS_PER_PGD is the number of pointers in the PGD, 1024 on an x86 without PAE. PTRS_PER_PMD is for the PMD, 1 on the x86 without PAE and PTRS_PER_PTE is for the lowest level, 1024 on the x86.
As mentioned, each entry is described by the structs pte_t, pmd_t and pgd_t for PTEs, PMDs and PGDs respectively. Even though these are often just unsigned integers, they are defined as structs for two reasons. The first is for type protection so that they will not be used inappropriately. The second is for features like PAE on the x86 where an additional 4 bits is used for addressing more than 4GiB of memory. To store the protection bits, pgprot_t is defined which holds the relevant flags and is usually stored in the lower bits of a page table entry.
For type casting, 4 macros are provided in asm/page.h, which takes the above types and returns the relevant part of the structs. They are pte_val(), pmd_val(), pgd_val() and pgprot_val(). To reverse the type casting, 4 more macros are provided __pte(), __pmd(), __pgd() and __pgprot().
Where exactly the protection bits are stored is architecture dependent. For illustration purposes, we will examine the case of an x86 architecture without PAE enabled but the same principles apply across architectures. On an x86 with no PAE, the pte_t is simply a 32 bit integer within a struct. Each pte_t points to an address of a page frame and all the addresses pointed to are guaranteed to be page aligned. Therefore, there are PAGE_SHIFT (12) bits in that 32 bit value that are free for status bits of the page table entry. A number of the protection and status bits are listed in Table ?? but what bits exist and what they mean varies between architectures.
Table 3.1: Page Table Entry Protection and Status Bits
These bits are self-explanatory except for the _PAGE_PROTNONE which we will discuss further. On the x86 with Pentium III and higher, this bit is called the Page Attribute Table (PAT) while earlier architectures such as the Pentium II had this bit reserved. The PAT bit is used to indicate the size of the page the PTE is referencing. In a PGD entry, this same bit is instead called the Page Size Exception (PSE) bit so obviously these bits are meant to be used in conjunction.
As Linux does not use the PSE bit for user pages, the PAT bit is free in the PTE for other purposes. There is a requirement for having a page resident in memory but inaccessible to the userspace process such as when a region is protected with mprotect() with the PROT_NONE flag. When the region is to be protected, the _PAGE_PRESENT bit is cleared and the _PAGE_PROTNONE bit is set. The macro pte_present() checks if either of these bits are set and so the kernel itself knows the PTE is present, just inaccessible to userspace which is a subtle, but important point. As the hardware bit _PAGE_PRESENT is clear, a page fault will occur if the page is accessed so Linux can enforce the protection while still knowing the page is resident if it needs to swap it out or the process exits.
Macros are defined in <asm/pgtable.h> which are important for the navigation and examination of page table entries. To navigate the page directories, three macros are provided which break up a linear address space into its component parts. pgd_offset() takes an address and the mm_struct for the process and returns the PGD entry that covers the requested address. pmd_offset() takes a PGD entry and an address and returns the relevant PMD. pte_offset() takes a PMD and returns the relevant PTE. The remainder of the linear address provided is the offset within the page. The relationship between these fields is illustrated in Figure 3.1.
The second round of macros determine if the page table entries are present or may be used.
There are many parts of the VM which are littered with page table walk code and it is important to recognise it. A very simple example of a page table walk is the function follow_page() in mm/memory.c. The following is an excerpt from that function, the parts unrelated to the page table walk are omitted:
407 pgd_t *pgd; 408 pmd_t *pmd; 409 pte_t *ptep, pte; 410 411 pgd = pgd_offset(mm, address); 412 if (pgd_none(*pgd) || pgd_bad(*pgd)) 413 goto out; 414 415 pmd = pmd_offset(pgd, address); 416 if (pmd_none(*pmd) || pmd_bad(*pmd)) 417 goto out; 418 419 ptep = pte_offset(pmd, address); 420 if (!ptep) 421 goto out; 422 423 pte = *ptep;
It simply uses the three offset macros to navigate the page tables and the _none() and _bad() macros to make sure it is looking at a valid page table.
The third set of macros examine and set the permissions of an entry. The permissions determine what a userspace process can and cannot do with a particular page. For example, the kernel page table entries are never readable by a userspace process.
The fourth set of macros examine and set the state of an entry. There are only two bits that are important in Linux, the dirty bit and the accessed bit. To check these bits, the macros pte_dirty() and pte_young() macros are used. To set the bits, the macros pte_mkdirty() and pte_mkyoung() are used. To clear them, the macros pte_mkclean() and pte_old() are available.
This set of functions and macros deal with the mapping of addresses and pages to PTEs and the setting of the individual entries.
The macro mk_pte() takes a struct page and protection bits and combines them together to form the pte_t that needs to be inserted into the page table. A similar macro mk_pte_phys() exists which takes a physical page address as a parameter.
The macro pte_page() returns the struct page which corresponds to the PTE entry. pmd_page() returns the struct page containing the set of PTEs.
The macro set_pte() takes a pte_t such as that returned by mk_pte() and places it within the processes page tables. pte_clear() is the reverse operation. An additional function is provided called ptep_get_and_clear() which clears an entry from the process page table and returns the pte_t. This is important when some modification needs to be made to either the PTE protection or the struct page itself.
The last set of functions deal with the allocation and freeing of page tables. Page tables, as stated, are physical pages containing an array of entries and the allocation and freeing of physical pages is a relatively expensive operation, both in terms of time and the fact that interrupts are disabled during page allocation. The allocation and deletion of page tables, at any of the three levels, is a very frequent operation so it is important the operation is as quick as possible.
Hence the pages used for the page tables are cached in a number of different lists called quicklists. Each architecture implements these caches differently but the principles used are the same. For example, not all architectures cache PGDs because the allocation and freeing of them only happens during process creation and exit. As both of these are very expensive operations, the allocation of another page is negligible.
PGDs, PMDs and PTEs have two sets of functions each for the allocation and freeing of page tables. The allocation functions are pgd_alloc(), pmd_alloc() and pte_alloc() respectively and the free functions are, predictably enough, called pgd_free(), pmd_free() and pte_free().
Broadly speaking, the three implement caching with the use of three caches called pgd_quicklist, pmd_quicklist and pte_quicklist. Architectures implement these three lists in different ways but one method is through the use of a LIFO type structure. Ordinarily, a page table entry contains points to other pages containing page tables or data. While cached, the first element of the list is used to point to the next free page table. During allocation, one page is popped off the list and during free, one is placed as the new head of the list. A count is kept of how many pages are used in the cache.
The quick allocation function from the pgd_quicklist is not externally defined outside of the architecture although get_pgd_fast() is a common choice for the function name. The cached allocation function for PMDs and PTEs are publicly defined as pmd_alloc_one_fast() and pte_alloc_one_fast().
If a page is not available from the cache, a page will be allocated using the physical page allocator (see Chapter 6). The functions for the three levels of page tables are get_pgd_slow(), pmd_alloc_one() and pte_alloc_one().
Obviously a large number of pages may exist on these caches and so there is a mechanism in place for pruning them. Each time the caches grow or shrink, a counter is incremented or decremented and it has a high and low watermark. check_pgt_cache() is called in two places to check these watermarks. When the high watermark is reached, entries from the cache will be freed until the cache size returns to the low watermark. The function is called after clear_page_tables() when a large number of page tables are potentially reached and is also called by the system idle task.
When the system first starts, paging is not enabled as page tables do not magically initialise themselves. Each architecture implements this differently so only the x86 case will be discussed. The page table initialisation is divided into two phases. The bootstrap phase sets up page tables for just 8MiB so the paging unit can be enabled. The second phase initialises the rest of the page tables. We discuss both of these phases below.
The assembler function startup_32() is responsible for enabling the paging unit in arch/i386/kernel/head.S. While all normal kernel code in vmlinuz is compiled with the base address at PAGE_OFFSET + 1MiB, the kernel is actually loaded beginning at the first megabyte (0x00100000) of memory. The first megabyte is used by some devices for communication with the BIOS and is skipped. The bootstrap code in this file treats 1MiB as its base address by subtracting __PAGE_OFFSET from any address until the paging unit is enabled so before the paging unit is enabled, a page table mapping has to be established which translates the 8MiB of physical memory to the virtual address PAGE_OFFSET.
Initialisation begins with statically defining at compile time an array called swapper_pg_dir which is placed using linker directives at 0x00101000. It then establishes page table entries for 2 pages, pg0 and pg1. If the processor supports the Page Size Extension (PSE) bit, it will be set so that pages will be translated are 4MiB pages, not 4KiB as is the normal case. The first pointers to pg0 and pg1 are placed to cover the region 1-9MiB the second pointers to pg0 and pg1 are placed at PAGE_OFFSET+1MiB. This means that when paging is enabled, they will map to the correct pages using either physical or virtual addressing for just the kernel image. The rest of the kernel page tables will be initialised by paging_init().
Once this mapping has been established, the paging unit is turned on by setting a bit in the cr0 register and a jump takes places immediately to ensure the Instruction Pointer (EIP register) is correct.
The function responsible for finalising the page tables is called paging_init(). The call graph for this function on the x86 can be seen on Figure 3.4.
Figure 3.4: Call Graph: paging_init()
The function first calls pagetable_init() to initialise the page tables necessary to reference all physical memory in ZONE_DMA and ZONE_NORMAL. Remember that high memory in ZONE_HIGHMEM cannot be directly referenced and mappings are set up for it temporarily. For each pgd_t used by the kernel, the boot memory allocator (see Chapter 5) is called to allocate a page for the PMDs and the PSE bit will be set if available to use 4MiB TLB entries instead of 4KiB. If the PSE bit is not supported, a page for PTEs will be allocated for each pmd_t. If the CPU supports the PGE flag, it also will be set so that the page table entry will be global and visible to all processes.
Next, pagetable_init() calls fixrange_init() to setup the fixed address space mappings at the end of the virtual address space starting at FIXADDR_START. These mappings are used for purposes such as the local APIC and the atomic kmappings between FIX_KMAP_BEGIN and FIX_KMAP_END required by kmap_atomic(). Finally, the function calls fixrange_init() to initialise the page table entries required for normal high memory mappings with kmap().
Once pagetable_init() returns, the page tables for kernel space are now full initialised so the static PGD (swapper_pg_dir) is loaded into the CR3 register so that the static table is now being used by the paging unit.
The next task of the paging_init() is responsible for calling kmap_init() to initialise each of the PTEs with the PAGE_KERNEL protection flags. The final task is to call zone_sizes_init() which initialises all the zone structures used.
There is a requirement for Linux to have a fast method of mapping virtual addresses to physical addresses and for mapping struct pages to their physical address. Linux achieves this by knowing where, in both virtual and physical memory, the global mem_map array is as the global array has pointers to all struct pages representing physical memory in the system. All architectures achieve this with very similar mechanisms but for illustration purposes, we will only examine the x86 carefully. This section will first discuss how physical addresses are mapped to kernel virtual addresses and then what this means to the mem_map array.
As we saw in Section 3.6, Linux sets up a direct mapping from the physical address 0 to the virtual address PAGE_OFFSET at 3GiB on the x86. This means that any virtual address can be translated to the physical address by simply subtracting PAGE_OFFSET which is essentially what the function virt_to_phys() with the macro __pa() does:
/* from <asm-i386/page.h> */
132 #define __pa(x) ((unsigned long)(x)-PAGE_OFFSET)
/* from <asm-i386/io.h> */
76 static inline unsigned long virt_to_phys(volatile void * address)
77 {
78 return __pa(address);
79 }
Obviously the reverse operation involves simply adding PAGE_OFFSET which is carried out by the function phys_to_virt() with the macro __va(). Next we see how this helps the mapping of struct pages to physical addresses.
As we saw in Section 3.6.1, the kernel image is located at the physical address 1MiB, which of course translates to the virtual address PAGE_OFFSET + 0x00100000 and a virtual region totaling about 8MiB is reserved for the image which is the region that can be addressed by two PGDs. This would imply that the first available memory to use is located at 0xC0800000 but that is not the case. Linux tries to reserve the first 16MiB of memory for ZONE_DMA so first virtual area used for kernel allocations is actually 0xC1000000. This is where the global mem_map is usually located. ZONE_DMA will be still get used, but only when absolutely necessary.
Physical addresses are translated to struct pages by treating them as an index into the mem_map array. Shifting a physical address PAGE_SHIFT bits to the right will treat it as a PFN from physical address 0 which is also an index within the mem_map array. This is exactly what the macro virt_to_page() does which is declared as follows in <asm-i386/page.h>:
#define virt_to_page(kaddr) (mem_map + (__pa(kaddr) >> PAGE_SHIFT))
The macro virt_to_page() takes the virtual address kaddr, converts it to the physical address with __pa(), converts it into an array index by bit shifting it right PAGE_SHIFT bits and indexing into the mem_map by simply adding them together. No macro is available for converting struct pages to physical addresses but at this stage, it should be obvious to see how it could be calculated.
Initially, when the processor needs to map a virtual address to a physical address, it must traverse the full page directory searching for the PTE of interest. This would normally imply that each assembly instruction that references memory actually requires several separate memory references for the page table traversal [Tan01]. To avoid this considerable overhead, architectures take advantage of the fact that most processes exhibit a locality of reference or, in other words, large numbers of memory references tend to be for a small number of pages. They take advantage of this reference locality by providing a Translation Lookaside Buffer (TLB) which is a small associative memory that caches virtual to physical page table resolutions.
Linux assumes that the most architectures support some type of TLB although the architecture independent code does not cares how it works. Instead, architecture dependant hooks are dispersed throughout the VM code at points where it is known that some hardware with a TLB would need to perform a TLB related operation. For example, when the page tables have been updated, such as after a page fault has completed, the processor may need to be update the TLB for that virtual address mapping.
Not all architectures require these type of operations but because some do, the hooks have to exist. If the architecture does not require the operation to be performed, the function for that TLB operation will a null operation that is optimised out at compile time.
A quite large list of TLB API hooks, most of which are declared in <asm/pgtable.h>, are listed in Tables 3.2 and ?? and the APIs are quite well documented in the kernel source by Documentation/cachetlb.txt [Mil00]. It is possible to have just one TLB flush function but as both TLB flushes and TLB refills are very expensive operations, unnecessary TLB flushes should be avoided if at all possible. For example, when context switching, Linux will avoid loading new page tables using Lazy TLB Flushing, discussed further in Section 4.3.
This flushes the entire TLB on all processors running in the system making it the most expensive TLB flush operation. After it completes, all modifications to the page tables will be visible globally. This is required after the kernel page tables, which are global in nature, have been modified such as after vfree() (See Chapter 7) completes or after the PKMap is flushed (See Chapter 9). This flushes all TLB entries related to the userspace portion (i.e. below PAGE_OFFSET) for the requested mm context. In some architectures, such as MIPS, this will need to be performed for all processors but usually it is confined to the local processor. This is only called when an operation has been performed that affects the entire address space, such as after all the address mapping have been duplicated with dup_mmap() for fork or after all memory mappings have been deleted with exit_mmap(). void flush_tlb_range(struct mm_struct *mm, unsigned long start, unsigned long end) As the name indicates, this flushes all entries within the requested userspace range for the mm context. This is used after a new region has been moved or changeh as during mremap() which moves regions or mprotect() which changes the permissions. The function is also indirectly used during unmapping a region with munmap() which calls tlb_finish_mmu() which tries to use flush_tlb_range() intelligently. This API is provided for architectures that can remove ranges of TLB entries quickly rather than iterating with flush_tlb_page().
Table 3.2: Translation Lookaside Buffer Flush API
Table 3.3: Translation Lookaside Buffer Flush API (cont)
As Linux manages the CPU Cache in a very similar fashion to the TLB, this section covers how Linux utilises and manages the CPU cache. CPU caches, like TLB caches, take advantage of the fact that programs tend to exhibit a locality of reference [Sea00] [CS98]. To avoid having to fetch data from main memory for each reference, the CPU will instead cache very small amounts of data in the CPU cache. Frequently, there is two levels called the Level 1 and Level 2 CPU caches. The Level 2 CPU caches are larger but slower than the L1 cache but Linux only concerns itself with the Level 1 or L1 cache.
CPU caches are organised into lines. Each line is typically quite small, usually 32 bytes and each line is aligned to it's boundary size. In other words, a cache line of 32 bytes will be aligned on a 32 byte address. With Linux, the size of the line is L1_CACHE_BYTES which is defined by each architecture.
How addresses are mapped to cache lines vary between architectures but the mappings come under three headings, direct mapping, associative mapping and set associative mapping. Direct mapping is the simpliest approach where each block of memory maps to only one possible cache line. With associative mapping, any block of memory can map to any cache line. Set associative mapping is a hybrid approach where any block of memory can may to any line but only within a subset of the available lines. Regardless of the mapping scheme, they each have one thing in common, addresses that are close together and aligned to the cache size are likely to use different lines. Hence Linux employs simple tricks to try and maximise cache usage
If the CPU references an address that is not in the cache, a cache missccurs and the data is fetched from main memory. The cost of cache misses is quite high as a reference to cache can typically be performed in less than 10ns where a reference to main memory typically will cost between 100ns and 200ns. The basic objective is then to have as many cache hits and as few cache misses as possible.
Just as some architectures do not automatically manage their TLBs, some do not automatically manage their CPU caches. The hooks are placed in locations where the virtual to physical mapping changes, such as during a page table update. The CPU cache flushes should always take place first as some CPUs require a virtual to physical mapping to exist when the virtual address is being flushed from the cache. The three operations that require proper ordering are important is listed in Table 3.4.
Flushing Full MM Flushing Range Flushing Page flush_cache_mm() flush_cache_range() flush_cache_page() Change all page tables Change page table range Change single PTE flush_tlb_mm() flush_tlb_range() flush_tlb_page()
Table 3.4: Cache and TLB Flush Ordering
The API used for flushing the caches are declared in <asm/pgtable.h> and are listed in Tables 3.5. In many respects, it is very similar to the TLB flushing API.
This flushes the entire CPU cache system making it the most severe flush operation to use. It is used when changes to the kernel page tables, which are global in nature, are to be performed. void flush_cache_mm(struct mm_struct mm) This flushes all entires related to the address space. On completion, no cache lines will be associated with mm. void flush_cache_range(struct mm_struct *mm, unsigned long start, unsigned long end) This flushes lines related to a range of addresses in the address space. Like it's TLB equivilant, it is provided in case the architecture has an efficent way of flushing ranges instead of flushing each individual page. void flush_cache_page(struct vm_area_struct *vma, unsigned long vmaddr) This is for flushing a single page sized region. The VMA is supplied as the mm_struct is easily accessible via vma→vm_mm. Additionally, by testing for the VM_EXEC flag, the architecture will know if the region is executable for caches that separate the instructions and data caches. VMAs are described further in Chapter 4.
Table 3.5: CPU Cache Flush API
It does not end there though. A second set of interfaces is required to avoid virtual aliasing problems. The problem is that some CPUs select lines based on the virtual address meaning that one physical address can exist on multiple lines leading to cache coherency problems. Architectures with this problem may try and ensure that shared mappings will only use addresses as a stop-gap measure. However, a proper API to address is problem is also supplied which is listed in Table 3.6.
Table 3.6: CPU D-Cache and I-Cache Flush API
Most of the mechanics for page table management are essentially the same for 2.6 but the changes that have been introduced are quite wide reaching and the implementations in-depth.
A new file has been introduced called mm/nommu.c. This source file contains replacement code for functions that assume the existence of a MMU like mmap() for example. This is to support architectures, usually microcontrollers, that have no MMU. Much of the work in this area was developed by the uCLinux Project (http://www.uclinux.org).
The most significant and important change to page table management is the introduction of Reverse Mapping (rmap). Referring to it as “rmap” is deliberate as it is the common usage of the “acronym” and should not be confused with the -rmap tree developed by Rik van Riel which has many more alterations to the stock VM than just the reverse mapping.
In a single sentence, rmap grants the ability to locate all PTEs which map a particular page given just the struct page. In 2.4, the only way to find all PTEs which map a shared page, such as a memory mapped shared library, is to linearaly search all page tables belonging to all processes. This is far too expensive and Linux tries to avoid the problem by using the swap cache (see Section 11.4). This means that with many shared pages, Linux may have to swap out entire processes regardless of the page age and usage patterns. 2.6 instead has a PTE chain associated with every struct page which may be traversed to remove a page from all page tables that reference it. This way, pages in the LRU can be swapped out in an intelligent manner without resorting to swapping entire processes.
As might be imagined by the reader, the implementation of this simple concept is a little involved. The first step in understanding the implementation is the union pte that is a field in struct page. This has union has two fields, a pointer to a struct pte_chain called chain and a pte_addr_t called direct. The union is an optisation whereby direct is used to save memory if there is only one PTE mapping the entry, otherwise a chain is used. The type pte_addr_t varies between architectures but whatever its type, it can be used to locate a PTE, so we will treat it as a pte_t for simplicity.
The struct pte_chain is a little more complex. The struct itself is very simple but it is compact with overloaded fields and a lot of development effort has been spent on making it small and efficient. Fortunately, this does not make it indecipherable.
First, it is the responsibility of the slab allocator to allocate and manage struct pte_chains as it is this type of task the slab allocator is best at. Each struct pte_chain can hold up to NRPTE pointers to PTE structures. Once that many PTEs have been filled, a struct pte_chain is allocated and added to the chain.
The struct pte_chain has two fields. The first is unsigned long next_and_idx which has two purposes. When next_and_idx is ANDed with NRPTE, it returns the number of PTEs currently in this struct pte_chain indicating where the next free slot is. When next_and_idx is ANDed with the negation of NRPTE (i.e. ∼NRPTE), a pointer to the next struct pte_chain in the chain is returned1. This is basically how a PTE chain is implemented.
To give a taste of the rmap intricacies, we'll give an example of what happens when a new PTE needs to map a page. The basic process is to have the caller allocate a new pte_chain with pte_chain_alloc(). This allocated chain is passed with the struct page and the PTE to page_add_rmap(). If the existing PTE chain associated with the page has slots available, it will be used and the pte_chain allocated by the caller returned. If no slots were available, the allocated pte_chain will be added to the chain and NULL returned.
There is a quite substantial API associated with rmap, for tasks such as creating chains and adding and removing PTEs to a chain, but a full listing is beyond the scope of this section. Fortunately, the API is confined to mm/rmap.c and the functions are heavily commented so their purpose is clear.
There are two main benefits, both related to pageout, with the introduction of reverse mapping. The first is with the setup and tear-down of pagetables. As will be seen in Section 11.4, pages being paged out are placed in a swap cache and information is written into the PTE necessary to find the page again. This can lead to multiple minor faults as pages are put into the swap cache and then faulted again by a process. With rmap, the setup and removal of PTEs is atomic. The second major benefit is when pages need to paged out, finding all PTEs referencing the pages is a simple operation but impractical with 2.4, hence the swap cache.
Reverse mapping is not without its cost though. The first, and obvious one, is the additional space requirements for the PTE chains. Arguably, the second is a CPU cost associated with reverse mapping but it has not been proved to be significant. What is important to note though is that reverse mapping is only a benefit when pageouts are frequent. If the machines workload does not result in much pageout or memory is ample, reverse mapping is all cost with little or no benefit. At the time of writing, the merits and downsides to rmap is still the subject of a number of discussions.
The reverse mapping required for each page can have very expensive space requirements. To compound the problem, many of the reverse mapped pages in a VMA will be essentially identical. One way of addressing this is to reverse map based on the VMAs rather than individual pages. That is, instead of having a reverse mapping for each page, all the VMAs which map a particular page would be traversed and unmap the page from each. Note that objects in this case refers to the VMAs, not an object in the object-orientated sense of the word2. At the time of writing, this feature has not been merged yet and was last seen in kernel 2.5.68-mm1 but there is a strong incentive to have it available if the problems with it can be resolved. For the very curious, the patch for just file/device backed objrmap at this release is available 3 but it is only for the very very curious reader.
There are two tasks that require all PTEs that map a page to be traversed. The first task is page_referenced() which checks all PTEs that map a page to see if the page has been referenced recently. The second task is when a page needs to be unmapped from all processes with try_to_unmap(). To complicate matters further, there are two types of mappings that must be reverse mapped, those that are backed by a file or device and those that are anonymous. In both cases, the basic objective is to traverse all VMAs which map a particular page and then walk the page table for that VMA to get the PTE. The only difference is how it is implemented. The case where it is backed by some sort of file is the easiest case and was implemented first so we'll deal with it first. For the purposes of illustrating the implementation, we'll discuss how page_referenced() is implemented.
page_referenced() calls page_referenced_obj() which is the top level function for finding all PTEs within VMAs that map the page. As the page is mapped for a file or device, page→mapping contains a pointer to a valid address_space. The address_space has two linked lists which contain all VMAs which use the mapping with the address_space→i_mmap and address_space→i_mmap_shared fields. For every VMA that is on these linked lists, page_referenced_obj_one() is called with the VMA and the page as parameters. The function page_referenced_obj_one() first checks if the page is in an address managed by this VMA and if so, traverses the page tables of the mm_struct using the VMA (vma→vm_mm) until it finds the PTE mapping the page for that mm_struct.
Anonymous page tracking is a lot trickier and was implented in a number of stages. It only made a very brief appearance and was removed again in 2.5.65-mm4 as it conflicted with a number of other changes. The first stage in the implementation was to use page→mapping and page→index fields to track mm_struct and address pairs. These fields previously had been used to store a pointer to swapper_space and a pointer to the swp_entry_t (See Chapter 11). Exactly how it is addressed is beyond the scope of this section but the summary is that swp_entry_t is stored in page→private
try_to_unmap_obj() works in a similar fashion but obviously, all the PTEs that reference a page with this method can do so without needing to reverse map the individual pages. There is a serious search complexity problem that is preventing it being merged. The scenario that describes the problem is as follows;
Take a case where 100 processes have 100 VMAs mapping a single file. To unmap a single page in this case with object-based reverse mapping would require 10,000 VMAs to be searched, most of which are totally unnecessary. With page based reverse mapping, only 100 pte_chain slots need to be examined, one for each process. An optimisation was introduced to order VMAs in the address_space by virtual address but the search for a single page is still far too expensive for object-based reverse mapping to be merged.
In 2.4, page table entries exist in ZONE_NORMAL as the kernel needs to be able to address them directly during a page table walk. This was acceptable until it was found that, with high memory machines, ZONE_NORMAL was being consumed by the third level page table PTEs. The obvious answer is to move PTEs to high memory which is exactly what 2.6 does.
As we will see in Chapter 9, addressing information in high memory is far from free, so moving PTEs to high memory is a compile time configuration option. In short, the problem is that the kernel must map pages from high memory into the lower address space before it can be used but there is a very limited number of slots available for these mappings introducing a troublesome bottleneck. However, for applications with a large number of PTEs, there is little other option. At time of writing, a proposal has been made for having a User Kernel Virtual Area (UKVA) which would be a region in kernel space private to each process but it is unclear if it will be merged for 2.6 or not.
To take the possibility of high memory mapping into account, the macro pte_offset() from 2.4 has been replaced with pte_offset_map() in 2.6. If PTEs are in low memory, this will behave the same as pte_offset() and return the address of the PTE. If the PTE is in high memory, it will first be mapped into low memory with kmap_atomic() so it can be used by the kernel. This PTE must be unmapped as quickly as possible with pte_unmap().
In programming terms, this means that page table walk code looks slightly different. In particular, to find the PTE for a given address, the code now reads as (taken from mm/memory.c);
640 ptep = pte_offset_map(pmd, address); 641 if (!ptep) 642 goto out; 643 644 pte = *ptep; 645 pte_unmap(ptep);
Additionally, the PTE allocation API has changed. Instead of pte_alloc(), there is now a pte_alloc_kernel() for use with kernel PTE mappings and pte_alloc_map() for userspace mapping. The principal difference between them is that pte_alloc_kernel() will never use high memory for the PTE.
In memory management terms, the overhead of having to map the PTE from high memory should not be ignored. Only one PTE may be mapped per CPU at a time, although a second may be mapped with pte_offset_map_nested(). This introduces a penalty when all PTEs need to be examined, such as during zap_page_range() when all PTEs in a given range need to be unmapped.
At time of writing, a patch has been submitted which places PMDs in high memory using essentially the same mechanism and API changes. It is likely that it will be merged.
Most modern architectures support more than one page size. For example, on many x86 architectures, there is an option to use 4KiB pages or 4MiB pages. Traditionally, Linux only used large pages for mapping the actual kernel image and no where else. As TLB slots are a scarce resource, it is desirable to be able to take advantages of the large pages especially on machines with large amounts of physical memory.
In 2.6, Linux allows processes to use “huge pages”, the size of which is determined by HPAGE_SIZE. The number of available huge pages is determined by the system administrator by using the /proc/sys/vm/nr_hugepages proc interface which ultimatly uses the function set_hugetlb_mem_size(). As the success of the allocation depends on the availability of physically contiguous memory, the allocation should be made during system startup.
The root of the implementation is a Huge TLB Filesystem (hugetlbfs) which is a pseudo-filesystem implemented in fs/hugetlbfs/inode.c. Basically, each file in this filesystem is backed by a huge page. During initialisation, init_hugetlbfs_fs() registers the file system and mounts it as an internal filesystem with kern_mount().
There are two ways that huge pages may be accessed by a process. The first is by using shmget() to setup a shared region backed by huge pages and the second is the call mmap() on a file opened in the huge page filesystem.
When a shared memory region should be backed by huge pages, the process should call shmget() and pass SHM_HUGETLB as one of the flags. This results in hugetlb_zero_setup() being called which creates a new file in the root of the internal hugetlb filesystem. A file is created in the root of the internal filesystem. The name of the file is determined by an atomic counter called hugetlbfs_counter which is incremented every time a shared region is setup.
To create a file backed by huge pages, a filesystem of type hugetlbfs must first be mounted by the system administrator. Instructions on how to perform this task are detailed in Documentation/vm/hugetlbpage.txt. Once the filesystem is mounted, files can be created as normal with the system call open(). When mmap() is called on the open file, the file_operations struct hugetlbfs_file_operations ensures that hugetlbfs_file_mmap() is called to setup the region properly.
Huge TLB pages have their own function for the management of page tables, address space operations and filesystem operations. The names of the functions for page table management can all be seen in <linux/hugetlb.h> and they are named very similar to their “normal” page equivalents. The implementation of the hugetlb functions are located near their normal page equivalents so are easy to find.
The changes here are minimal. The API function flush_page_to_ram() has being totally removed and a new API flush_dcache_range() has been introduced.


