No.
Suppose that a successful run takes one week, but that a failure takes on average almost zero time. Then the optimal approach is to test the commits linearly starting from the known-bad commit and moving towards the known-good commit. This will take one week, because you will have but one successful test run, and the failures cost you (almost) nothing. In contrast, bisection will likely result in multiple successful test runs, costing multiple weeks.
For a less-extreme example, suppose that a successful run takes ten hours, but that a failure takes only one hour on average, and that there are 35 commits to search. Then the optimal power-search technique would weight the bad commit by a four-to-one ratio, so that the next commit to test is four times closer to the bad commit than to the good commit. Larger numbers of commits increase the weighting somewhat. The expected search time is decreased by about 25%, which might not be worthwhile in many cases, but is quite helpful when faced with ten-hour runs. The exact value of the weighting is not critical, as can be seen in the following plot, which shows the expected costs of power-search of 35, 128, and 1024 commits with varying weightings. A weighting of 10 puts the new commit ten times closer to the bad (cheap to test) commit than to the good (expensive to test) commit.
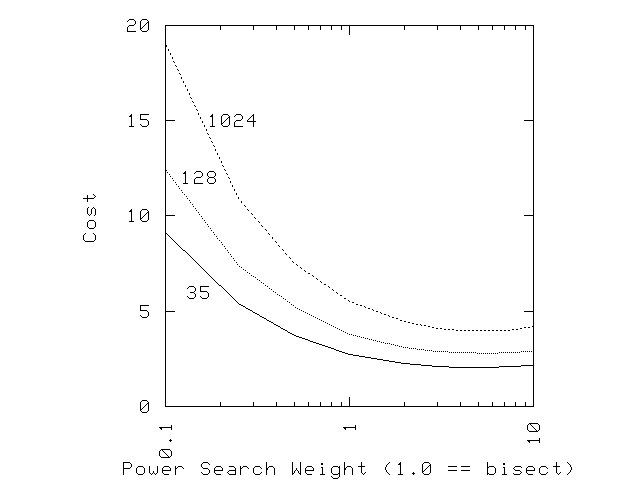
The code producing the data for this plot is available under GPL.
Of course, if you have machines to spare, you might consider using three machines in parallel by quadrisecting rather than bisecting. Quadrasecting allows you to double the convergence rate, although at the cost of tripling the hardware dedicated to the task. Similarly, you could apply seven machines via octasecting, tripling the convergence rate over that of bisection at a seven-fold increase in machines.
As machine prices contine to decrease and test cases continue to lengthen, quadrisection and octasection will likely become increasingly attractive, though it seems unlikely that these techniques would ever completely replace bisection.